Flores y Fibonacci
Esta semana en el Podcast en el que participamos (No me cuentes Historias) hablamos de la revolución de los claveles, con sus icónicas imágenes de soldados con claveles en los cañones.

Y me vino a la mente otra imagen icónica y es la de la revolución flower power. Seguro que os suena una foto donde una estudiante hippie ofreció una margarita a los soldados que les apuntaban.

Así que las flores se han usado en varias revoluciones y de flores venimos a hablaros hoy.
No sé si os sonará Fibonacci, también conocido como Leonardo de pisa. Seguro que sí. En un artículo anterior os contamos que fue quien introdujo el cero en Europa en el siglo XII. Si no, quedaros con su nombre porque seguro que vuelve a salir, ya que sus aportes a las Matemáticas fueron muchos.
Pero, ¿qué tiene que ver Fibonacci con las flores?
Pues bien, existe una sucesión numérica conocida como la sucesión de Fibonacci, porque fue él el que la descubrió, que se repite a menudo en la naturaleza.
La sucesión se crea empezando por el 0, el 1 y a partir de ahí vamos sumando los dos términos anteriores: 0+1=1, 1+1= 2, 2+1=3…
Así los primeros términos de la serie serían:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987…
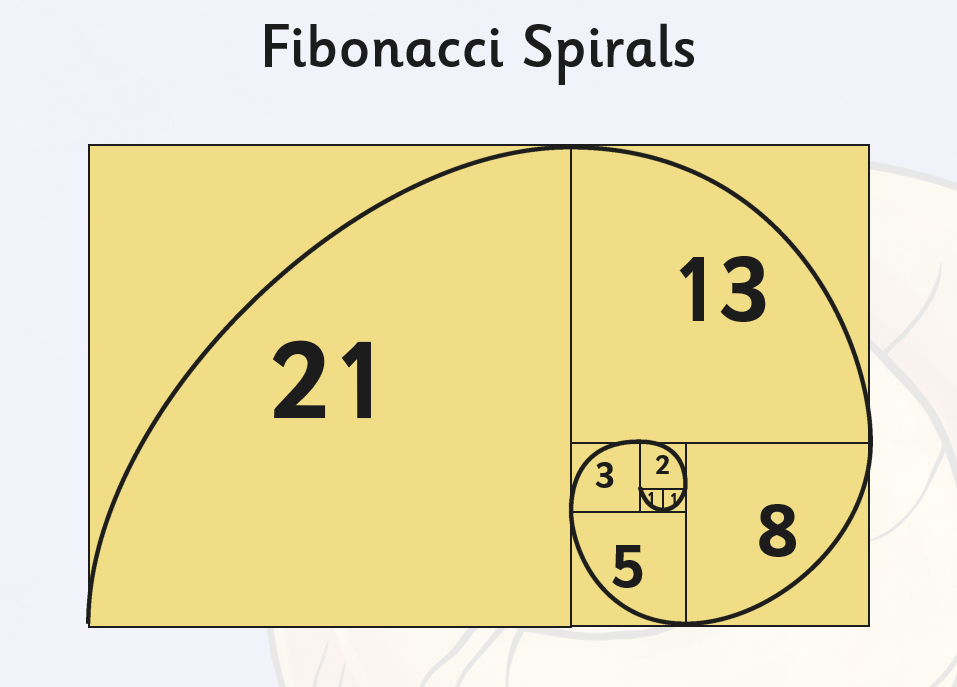
Esta sucesión tiene una particularidad y es que si dividimos un término por su anterior nos saldrá el número de oro, phi (1,61803…), que es un número irracional. De este número ya os hemos hablado también puesto que es un número muy especial representa la proporción áurea.
Volvemos a la sucesión de Fibonacci y los pétalos y es que resulta que la mayoría de flores tienen un número de pétalos igual a uno de los números que aparecen en la sucesión de Fibonacci.
El lirio de la paz o el anturium rojo solo tienen 1 pétalo, también encontramos lirios, orquídeas y campanillas de 3 pétalos. La mayor parte de geranios, violetas, azaleas y orquídeas tienen 5 pétalos. También es habitual encontrar flores de 8, 13 o 21 pétalos. E incluso hay una flor conocida como la flor de los mil pétalos: la peonía. Aunque yo apostaría a que muchas peonias tienen 987 pétalos ;).

Pero esto que os contamos no quiere decir que no puedan existir flores que tengan un número de pétalos que no esté en la sucesión de Fibonacci, de hecho existen flores de 4 pétalos como las plumerias. Pero que la mayoría de flores lo cumplirán, os reto a que vayáis por el campo contando pétalos de flores y nos contáis los resultados.
RELACIÓN CON EL JUEGO DE DESHOJAR MARGARITAS (ME QUIERE O NO ME QUIERE)
Volviendo a las margaritas, que son icono del movimiento hippie, vamos a contaros otra curiosidad. Como el resto de flores también se puede relacionar los pétalos con la sucesión. De hecho, la mayoría de margaritas tienen números pertenecientes a la sucesión de Fibonacci: 13, 21,34, o incluso algunas más pobladas de 55 y 89 pétalos.


Por tanto, si nos fijamos 4 de los cinco números más comunes para estas flores son impares (13, 21, 55 y 89). Así que cuando jugamos al juego de «me quiere», «no me quiere», como empezamos por el «me quiere» y la mayoría de margaritas tienen un número impar, pues la mayoría de veces nos saldrá que nos quieren.
A que ahora entendéis porque jugamos a este juego y es que seguramente obtendremos el resultado que necesitamos y queremos escuchar.
Muy atentos a la sucesión de Fibonacci y a su proporción áurea porque son claves en la naturaleza.
SALUDOS DESDE EL INFINITO
Bibliografía
- https://matematicascercanas.com/2014/11/21/me-quiere-no-me-quiere-me-quiere/
- https://www2.ual.es/jardinmatema/sucesion-de-fibonacci/
- Rocha, M. I. V. (2006). La sucesión de Fibonacci. Revista de Educación Matemática (RevEM), 21(3), 3. https://revistas.unc.edu.ar/index.php/REM/article/view/10717
- Hernández Fenollosa, MDLÁ. (2019). La serie de Fibonacci. http://hdl.handle.net/10251/121662
- Ferrando, I., & Segura, C. (2010). La sucesión de Fibonacci como herramienta para modelizar la naturaleza. Modelling in science education and learning, 3, 45-54. http://polipapers.upv.es/index.php/MSEL/article/view/3111/3204
- SANCHEZ RIVERA, A. C., & TOVAR VANEGAS, D. F. (2014). APLICACIONES Y CURIOSIDADES DE LOS NUMEROS DE FIBONACCI (Doctoral dissertation, UNIVERSIDAD SURCOLOMBIANA).
- Gallego, F. B. (2005). Ubicuidad de la sucesión de Fibonacci. In Un breve viaje por la ciencia (pp. 49-54). Universidad de La Rioja.
- https://www.twinkl.es/teaching-wiki/fibonacci-sequence

