HISTORIA DE LOS PUZZLES. EL OSTOMACHION

Buenas a todos, el artículo de hoy nos enloquece y es que…¿Puede haber algo más matemático que los puzzles? Con ellos se trabaja la lógica, la visión espacial, la resolución de problemas, la atención , la concentración, entre otras. Por ello los puzzles son aconsejables para cualquier edad y en cualquiera de sus formatos.

Salimos hablando de ello en el programa 67 del podcast “No me cuentes historias” por si os apetece escuchar un resumen de este artículo y otras curiosidades sobre rompecabezas

¿Qué entendemos por puzzle?

Si buscáis la definición de puzzle en la RAE te redirige a Rompecabezas y la primera acepción es:

Juego que consiste en componer determinada figura combinando cierto número de pedazos de madera o cartón, en cada uno de los cuales hay una parte de la figura.

La segunda acepción, que viene del habla coloquial es:

Problema o acertijo de difícil solución.

Y la tercera definición de un rompecabezas es:

Arma ofensiva compuesta de dos bolas de hierro o plomo sujetas a los extremos de un mango corto y flexible.

Es un arma parecida al mayal, esta definición la podemos dejar para usarla cuando digáis que no os gustan las matemáticas.

Hacer puzzles puede ser como una especie de meditación, que puede tranquilizar y relajar. La diversión reside en el reto que supone el proceso y no tanto en el resultado. ¡Como si queremos desmontarlos al acabar! Si nunca habéis usado un puzzle como una herramienta de meditación y estáis estresados y creeis que meditar no es para vosotros porque os desconcentráis en seguida, intentad hacer un puzzle y descubriréis que es un tiempo para vosotros, para desconectar. Podéis hacer 10 minutos al día hasta que lo acabéis.

Los orígenes del puzzle

John Spilsbury es considerado el padre de los puzzles modernos, en lo que pensamos al oír la palabra Puzzle. Los creó para propósitos educativos, y los llamó “Mapas diseccionados”. En 1766 hizo un mapa mundial de madera y recortó cada país como herramienta educativa para enseñar Geografía. Pensó que podía ser un buen negocio y montó una empresa para venderlos. En la imagen podemos ver el Puzzle de Europa

Pero podemos encontrar puzzles mucho más lejos en el tiempo y es que hoy vamos a hablaros sobre el Ostomachion o loculus Archimedius. Tranquilos, ¡¡no son palabrotas!! Ostomachion viene de “lucha de huesos”, ya que las piezas del juego se construían con ese material.

El Ostomachion o loculus Archimedius

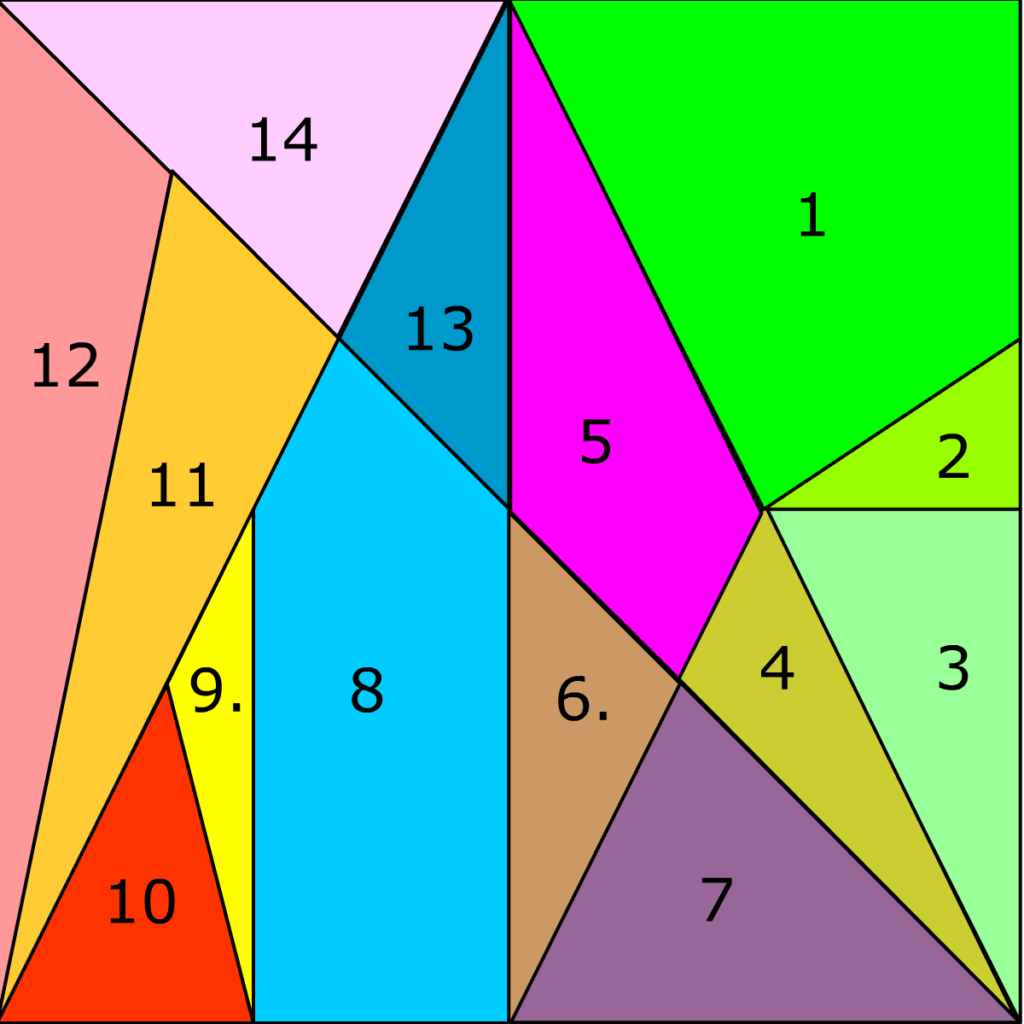
El juego es un rompecabezas geométrico compuesto por 14 piezas. En concreto, 11 triángulos, 2 cuadriláteros y 1 pentágono, que se unen formando un cuadrado. En la siguiente imagen se ve una descomposición de sus piezas.

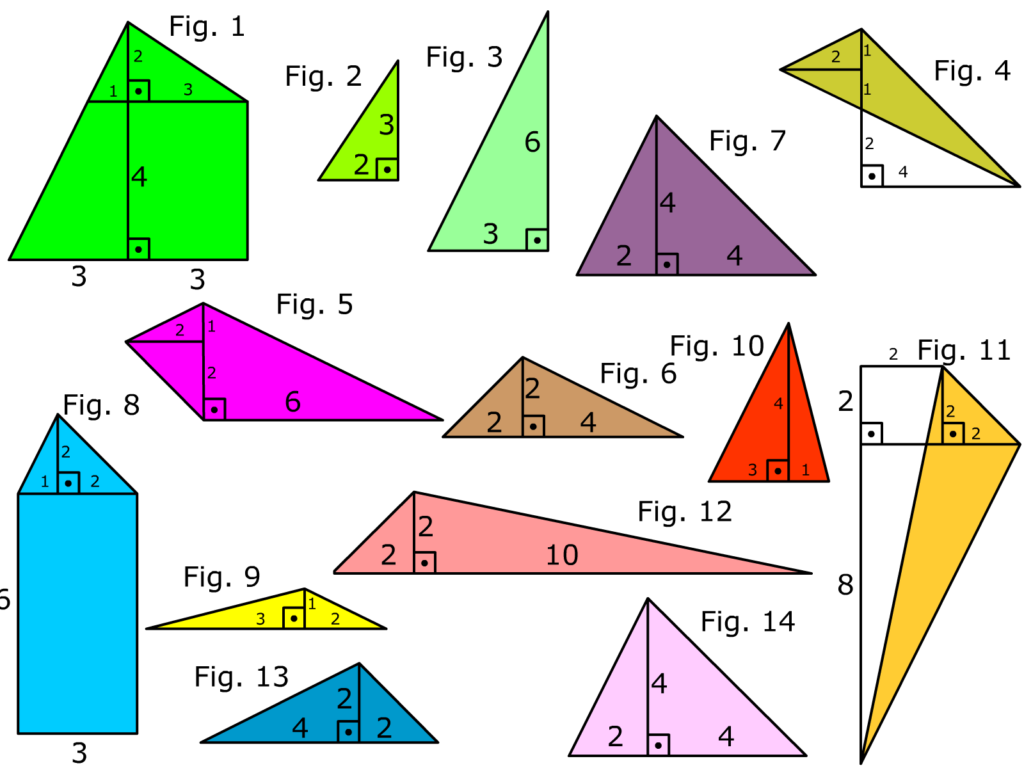
Descomposición del Ostomachion por piezas^{Wikimedia Commons}

Parece que se podía jugar por parejas. Pero una curiosidad es que una forma de jugar que atestiguan los textos clásicos es la creación de diferentes objetos, animales o plantas al reorganizar las piezas: un elefante, un árbol, un perro ladrando, un barco, una espada, una torre… Vamos, que es un Tangram versión pro.

El Tangram es un juego chino muy antiguo llamado «Chi Chiao Pan» que significa «juego de los siete elementos» o «tabla de la sabiduría». Existen varias versiones sobre el origen de la palabra Tangram, una de las más aceptadas cuenta que la palabra la inventó un inglés uniendo el vocablo cantones «tang» que significa chino con el vocablo latino «gram» que significa escrito o gráfico.

Otra versión narra que el origen del juego se remonta a los años 618 a 907 de nuestra era, época en la que reinó en China la dinastía Tang de donde se derivaría su nombre

No se sabe con certeza quién inventó el juego ni cuándo, pues las primeras publicaciones chinas en las que aparece el juego datan del siglo XVIII, época para la cual el juego era ya muy conocido en varios países del mundo.

Ya le dedicaremos otro artículo completo al Tangram, pero hoy estamos aquí para contaros más del Ostomachion, que es más desconocido y resulta muy interesante para el estudio de la Combinatoria.

El Ostomachion o caja de Arquímedes es un rompecabezas milenario, y es que está recogido en el palimpsesto de Arquímedes. Debemos pensar que Arquimedes es un matemático griego que vivió en el siglo III a.C. a quien se atribuye la frase “dadme un punto de apoyo y levantaré el mundo”.

Pero antes de entrar en materia, un palimpsesto es un “manuscrito antiguo que conserva huellas de una escritura anterior borrada artificialmente para su reutilización”. Los soportes en papiro o papel eran carísimos en la antigüedad,así que se reutilizaban borrando el original ya fuese mediante el raspado de la tinta con algún material, como la piedra pómez, o utilizando alguna sustancia ácida, como el jugo de naranja, que borrase el texto.

Pero con las técnicas modernas se han podido recuperar partes de algunos palimpsestos. Y es el caso de El Palimpsesto de Arquímedes, que con anterioridad a ser borrado era un manuscrito escrito en griego en el siglo X, copia de una recopilación de obras de Arquímedes para su conservación. Pero en el siglo XIII un monje cristiano separó sus folios, raspó y lavó para convertirlo en un texto litúrgico.

Como hemos dicho con los métodos modernos se han podido recuperar algunas partes de la colección que habían copiado de Arquímedes, en ella aparecen tratados sobre el equilibrio de los planos, sobre la esfera y el cilindro, sobre los cuerpos flotantes e incluso copias únicas existentes como la del “Método de los Teoremas mecánicos” o la obra más completa sobre el Ostomachion de este genio de las matemáticas.

No se sabe qué es más antiguo, si el juego o la investigación geométrica de Arquímedes sobre la figura del Ostomachion. Podría ser que Arquímedes no lo inventase y se limitará a hacer algunas reflexiones matemáticas sobre el mismo y es que volviendo a compararlo con el Tangram:

En el rompecabezas llamado Tangram solo hay una forma de armar un cuadrado con sus 7 piezas (sin contar rotaciones, reflexiones o cambiar figuras iguales) mientras que en el Ostomachion existen muchísimas soluciones y es sobre lo que trataba el tratado de Arquimedes, sobre combinatoria y las múltiples posibilidades que hay.

No penséis que os podéis sentar una tarde con el puzzle de Arquímedes y sacar todas sus soluciones. En una investigación publicada en 2003 por el Doctor Dr. Reviel Netz de la Universidad de Stanford, que argumentaba que Arquímedes estaba intentando determinar en cuántas formas se podía ensamblar las piezas para formar un cuadrado, se demostró que se podían obtener 536 combinaciones distintas. Que además, se elevarían a 17.152 si contáramos con las rotaciones de piezas, las reflexiones (es decir, giro en espejo) o los intercambios de piezas iguales.

En la siguiente imagen podéis ver algunos ejemplos de sus combinaciones:

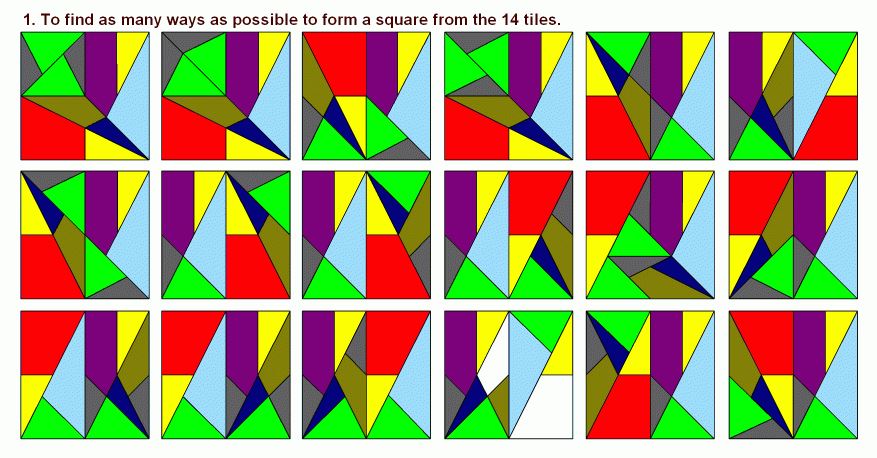
^{Imágen extraida de: https://www.craftsmanspace.com/free-projects/stomachion-of-archimedes-puzzle-plan.html}

Y si os cuesta creer que existen 536 distintas combinaciones para formar el cuadrado mirar la imagen que hemos encontrado en el repositorio de Amazon donde aparecen todas (13 columnas x 12 filas) menos los 16 huecos de las esquinas.

^{536 COMBINACIONES DISTINTAS DEL OSTOMACHION}

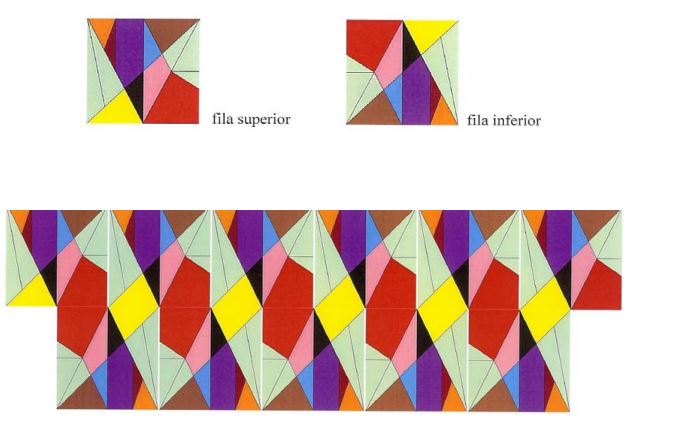
¿Y cómo puede ser que si incluimos rotaciones, reflexiones e intercambio de piezas pasemos de 536 soluciones a 17.152?

Si nos fijamos en la siguiente imagen, para una solución tenemos 4 rotaciones (fila superior) y 4 reflexiones (fila inferior) como un espejo. Y a su vez hay 2 parejas de piezas iguales que se pueden intercambiar (piezas 7-14 y piezas 6-13) dando 4 combinaciones más. 536 soluciones por 8 rotaciones, reflexiones y por 4 intercambios nos da las 17.152 combinaciones posibles.

Ahora vamos a jugar un poco más, haciendo algunos cálculos con el Ostomachion

Calcular el área de las piezas del ostomachión

Si consideramos que el cuadrado tiene unas dimensiones de 12 unidades de Longitud (podemos pensar en metros, centímetros o pulgadas, o simplemente unidades, lo que más cómodo e intuitivo nos resulte) de lado e inscribimos el Ostomachion en una cuadrícula de 12u x 12u nos será fácil calcular el área de cada pieza. Podría ser un ejercicio bueno para el estudio y la práctica de la geometría o para demostrar el Teorema de Pick (esto será otro artículo).

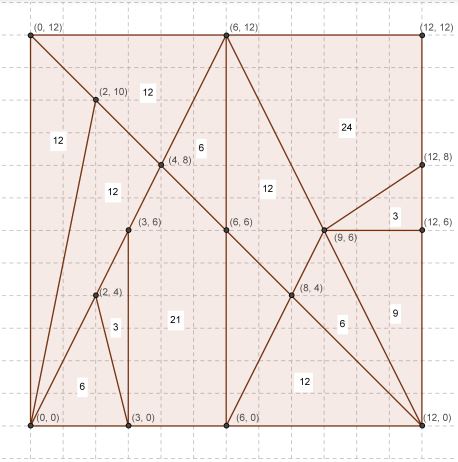
^{Imagen extraida de: https://trepo.tuni.fi/bitstream/handle/10024/95937/GRADU-1405404556.pdf?sequence=1&isAllowed=y}

Hay múltiples formas de calcular las áreas de cada figura, pero os vamos a enseñar una y os dejamos que penséis las demás o que probéis a calcularlas con el Teorema de Pick. Así, vamos a calcular el área de la pieza más grande, el cuadrilátero de la esquina superior derecha en la imagen anterior.

Una forma de calcular el área sería subdividir la imagen según nos interese, como por ejemplo:

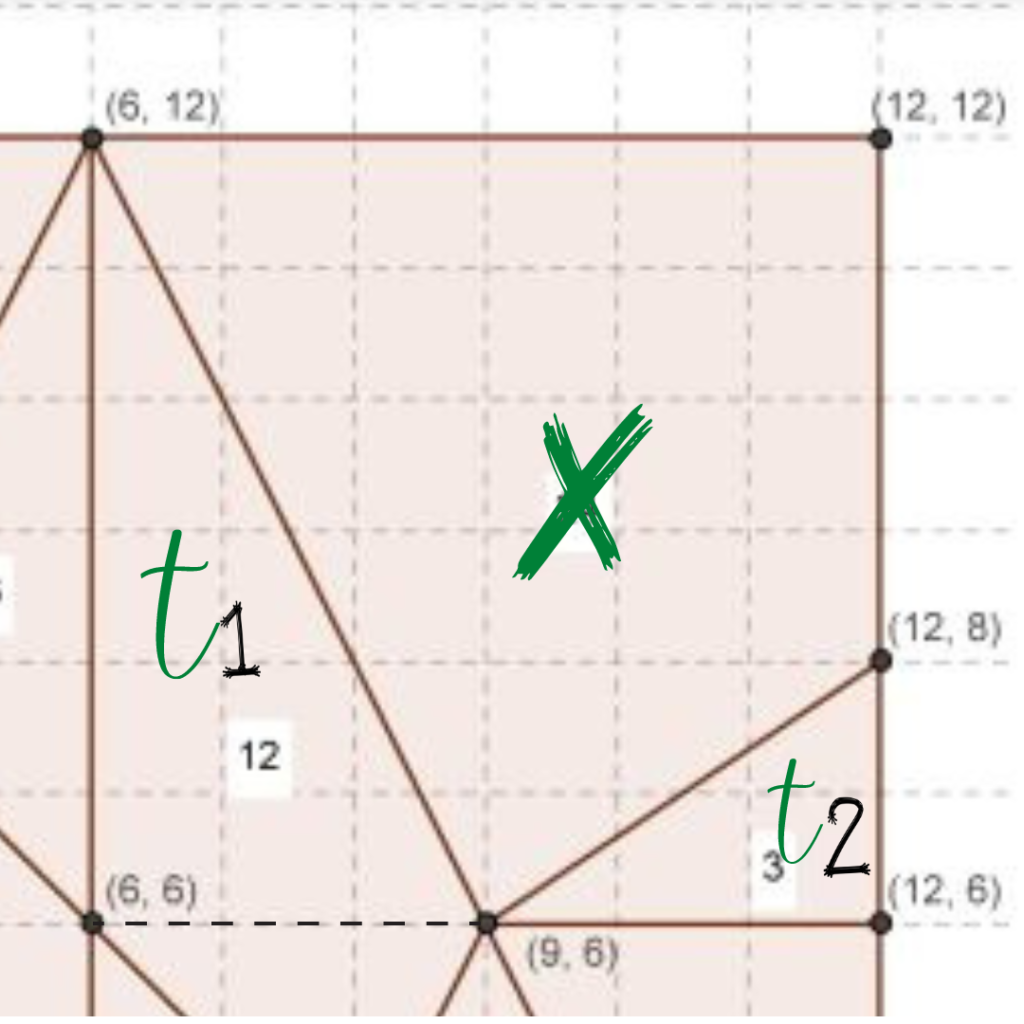
La sección elegida es un cuadrado de lado 6 unidades y por tanto su área será:

Los triángulos t1 y t2 son triángulos rectángulos y sus áreas son muy sencillas:

De esta forma el área del cuadrilátero marcado como x será:

Os animamos a dejarnos más formas de sacar el área de esa pieza que hemos llamado «x» en los comentarios.

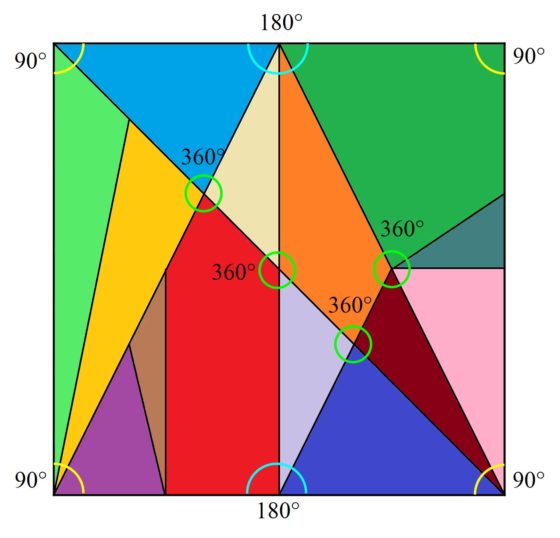
Tal como podemos ver en la siguiente imagen el Ostomachion sería también un buen recurso para trabajar Trigonometría: senos, cosenos, tangentes, ángulos complementarios, suplementarios… Pero eso lo dejaremos para otra ocasión.

^{Imágen extraida de https://culturacientifica.com/2019/11/06/el-puzzle-stomachion-y-el-palimpsesto-de-arquimedes-2/}

Usos de la caja de Arquímedes

Se puede usar para jugar como el Tangram, para buscar combinaciones de cuadrados o como hemos visto para trabajar Geometría y Trigonometría. E incluso para arquitectura o diseño tanto en 2D como en 3D. Como siempre Arte y Matemáticas van de la mano (algún día le dedicaremos un artículo completo a esta afirmación).

Mirad que imagen más chula para un mosaico:

O esta otra imagen de una composición en 3D:

Estas 2 últimas imágenes están sacadas de un artículo para unas Jornadas Internacionales (Matemáticas everywhere) titulado «Jugando con Arquímedes» de Juana María Sanchez, de la Universidad Politécnica de Madrid.

Esperamos que os pongáis a hacer puzzles ya. Hasta la próxima.

Saludos desde el infinito

Bibliografía