MATEMÁTICAS Y COLOR

Aquí estamos otra vez con nuestras curiosidades matemáticas, como ya sabéis aparecemos cada 15 días en el Podcast No me cuentes historias haciendo divulgación sobre nuestra pasión. En este caso el programa trata sobre el Blue Monday y os recomendamos que los escuchéis aquí.

En el programa se habla del nacimiento del Blue Monday, la teoría del color y la psicología del color, entre otras cosas. Y desde El Aprobatorio aportamos nuestro granito de conocimiento con curiosidades sobre Matemáticas y Color. Aquí va una ampliación de lo que se comenta en el programa:

¿De qué color son las Matemáticas?

Las matemáticas pueden ser de muchos colores: negras para algunos, o rojas, en función del color con el que el profesor pusiera las notas, o verdes como la naturaleza ya que forman parte de todo, o azules como algunos libros de texto.

Y sobre el color de las carpetas, cuadernos y libros de matemáticas hay un gran debate, de hecho hasta Ibai ha escrito su opinión en Twitter sobre este tema, dándole el azúl a las Matemáticas.

Parece que el mayor debate se centra entre si deberían ser rojas o azules. A raíz de unos cuadernos de la marca Oxford también nos encontramos con un extenso debate en Twitter, parecido al de la tortilla de patatas con o sin huevo ¿Pero por qué rojo o azul y no amarillo?

Si pensamos en la psicología del color, se considera que el rojo está asociado con temas que podrían ser bastante difíciles, ya que el color rojo en sí mismo está asociado con emociones fuertes como la tensión, la ira y la hostilidad. Y las matemáticas se consideran una materia difícil para la mayoría de las personas, por lo que tienden a etiquetarse como «rojas».

Sin embargo, la otra opinión popular de que las matemáticas son azules es probablemente para aquellos estudiantes que disfrutan de las matemáticas o que son buenos en ellas, ya que el azul se considera un color tranquilo y relajante. De hecho, el color azul se asocia con las matemáticas porque es un color técnico frío sin emociones y representa el tipo de materia técnica que se basa principalmente en hechos y lógica.

¿Qué opinais vosotros? ¿de qué color son las Matemáticas? Podéis dejar vuestros comentarios.

Pero hablando de temas más técnicos…

¿Qué relación hay entre las Matemáticas y el Color?

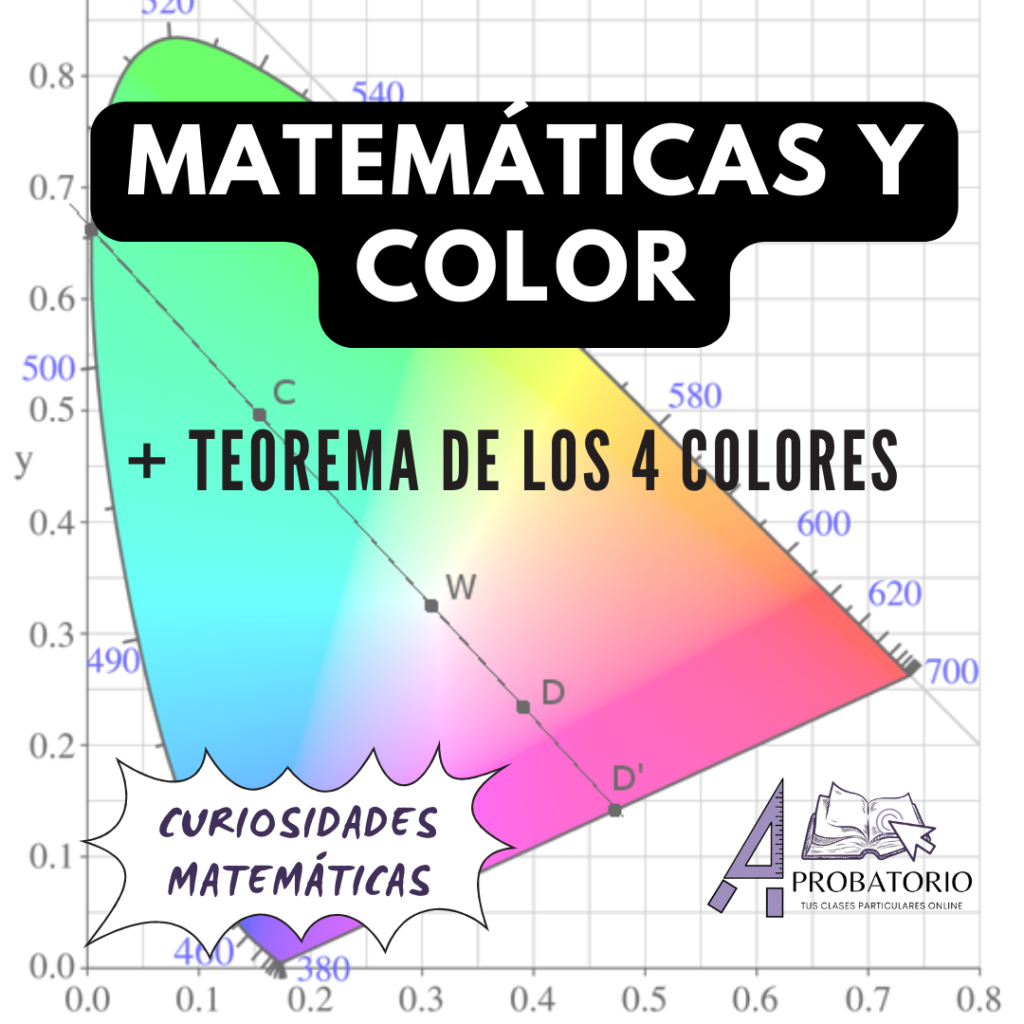
Nadie puede dudar de su relación cuando vemos un diagrama de cromoticidad. El diagrama cromático, introducido experimentalmente y estadísticamente por el CIE (Commission Internationale del Eclairage) el 1931, es una forma muy clara de representar los colores en el plano. Se usan unas coordenadas x e y basadas en los colores imaginarios a, b y c. Entonces, los colores reales se representan por puntos de este plano.

Se pueden asignar colores aproximados a áreas del diagrama de cromaticidad CIE. Estas son categorías aproximadas y no deben tomarse como afirmaciones precisas de color. Los bordes y los nombres de colores son una adaptación de Brand Fortner, «Number by Color», Part 5, SciTech Journal 6, p32, May/June 1996.

No vamos a entrar en detalle, pero el color está relacionado con la luz y su comportamiento en forma de onda, es decir, tendremos que hablar de frecuencia y las veces que vibra un objeto por segundo.También debemos relacionar el color con conceptos como el brillo, el tono, la saturación.

La luminosidad o brillo es la cantidad de luz emitida o reflejada por un objeto. Y en un color sería su claridad u oscuridad.
El tono sería lo que normalmente entendemos cuando nos referimos popularmente al color. Técnicamente podríamos decir que el tono es la longitud de onda dominante del color que vemos.
La saturación define la intensidad o grado de pureza de cada color. Sus valores se mueven desde su máximo, cualquier color puro, hasta su mínimo que corresponde a un tono grisáceo. Cuando coloquialmente decimos que un color es muy vivo o intenso nos estamos refiriendo a que está muy saturado.

Para elegir un solo color tenemos que definir estos tres parámetros, cualquiera que haya trabajado con Photoshop entiende la gran relación existente entre el color y las Matemáticas.

Los diseñadores usan esquemas de color RGB (red, green, blue) y CMYK (Cyan, Magenta, Yellow y Key, que representa al negro) para mezclar colores. Mientras que el primero es para visualización en computadoras, el segundo es para medios impresos.

Y volviendo a las matemáticas, existen modelos de colores aditivos y sustractivos, así en el modelo CMYK los tres colores primarios se restan para conseguir el negro (Key) en el centro y el blanco significaria la ausencia de color, por tanto es un modelo sustractivo. Mientras que en el modelo RGB los tres colores se suman para producir el blanco, siendo este un modelo aditivo, donde el negro implicaria la ausencia de color.

Y por último os contaremos un teorema muy curioso relacionado con colores:

EL TEOREMA DE LOS CUATRO COLORES

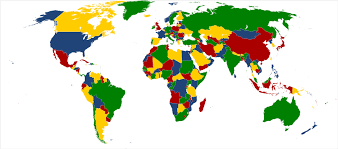
El teorema de los cuatro colores dice que: Dado cualquier mapa geográfico con regiones continuas, éste puede ser coloreado con cuatro colores diferentes, de forma que no queden regiones adyacentes (es decir, regiones que compartan no sólo un punto, sino todo un segmento de borde en común) con el mismo color.

Un poco de Historia

Este teorema se enunció en forma de conjetura en 1852. Nació cuando el matemático y botánico Francis Guthrie observó que era capaz de colorear un mapa complicado de los cantones de Inglaterra con sólo 4 colores. A raíz de eso postuló que estos cuatro colores serían suficientes para colorear cualquier mapa sin que dos regiones que comparten frontera tuvieran el mismo color.

Les planteó el problema a su hermano Frederick y a Augustus de Morgan, el cual mostró un gran interés por la conjetura y la difundió a sus colegas matemáticos, hasta que en 1978 Arthur Cayle publicó el enunciado de la conjetura preguntando en un encuentro que si alguien lo había resuelto ya.

En 1879 Sir Alfred Bray Kempe publicó su demostración que fue aceptada y pasó a ser folklore matemático para hacer puzzles y juegos. Pero en 1890 Joh Heawood encontró un caso en el que la demostración de Kempe no funcionaba. Aunque no quiere decir que la conjetura fuera falsa, solo que no estaba demostrada.

Y un siglo más tarde, en 1976, Appel y Haken llegan a la demostración con la ayuda de un ordenador, siendo el primer Gran Teorema probado usando un ordenador, aunque no sin controversia.

De hecho aún hoy los escépticos ponen en duda el uso de ordenadores para demostraciones, por varias razones como el aspecto de la comprobabilidad que pone en duda la credibilidad de la prueba al no poder ser comprobado por una persona.

¿Qué creeis vosotros? ¿Está demostrado?

Y mientras lo pensamos porque no lo comprobamos en este mapa de regiones:

O un poco más entretenido, en este mapa de provincias:

Os dejamos coloreando…

SALUDOS DESDE EL INFINITO

Fuentes de información